Introducción a la Estadística

¿Alguna vez te has preguntado cómo los científicos llegan a conclusiones confiables? La estadística es tu respuesta. Es la ciencia que te permite analizar datos y tomar decisiones basadas en evidencia real.

Este material cubre desde conceptos básicos hasta técnicas avanzadas. Vas a aprender sobre población y muestra (la diferencia entre estudiar a todos vs. estudiar a unos cuantos), parámetros y estimadores (valores reales vs. calculados), y tipos de variables.

Las variables pueden ser continuas (como peso o altura que se pueden dividir infinitamente) o discretas (como número de estudiantes que solo pueden ser números enteros). También estudiarás medidas de tendencia central (media, mediana, moda) y medidas de dispersión (qué tan esparcidos están tus datos).

Consejo clave: Dominar estos conceptos básicos te dará una base sólida para todo lo que viene después.

Estimadores Básicos con Ejemplo Práctico

Imagínate que eres un campesino que cosecha manzanas durante tres días: 1 kg, 2 kg, y 3 kg. Con estos datos simples vas a entender conceptos fundamentales que te servirán para análisis más complejos.

La media muestral (x̄) se calcula sumando todos los valores y dividiendo entre el número de datos: (1+2+3)/3 = 2 kg. Esta es tu medida de tendencia central más importante.

La variación te dice qué tanto se alejan tus datos de la media. Calculas las desviaciones restando cada dato de la media: (1-2)=-1, (2-2)=0, (3-2)=1. Al sumar estas desviaciones siempre obtienes cero, por eso necesitas elevarlas al cuadrado.

Dato importante: Las unidades cambian con los cálculos - si tu media está en kg, tu varianza estará en kg².

Visualización de la Variación

Los gráficos de dispersión te ayudan a ver patrones que los números solos no revelan. Cuando graficas tus datos, la media aparece como una línea horizontal que pasa por el centro de los puntos.

Las desviaciones son las distancias desde cada punto hasta esa línea horizontal. Algunas son positivas, otras negativas, pero todas te dicen qué tan dispersos están tus datos.

Cuando elevas al cuadrado estas desviaciones eliminas los valores negativos. La suma de estas desviaciones al cuadrado te da información crucial sobre la variabilidad de tu muestra.

Recuerda: Este procedimiento de calcular desviaciones será fundamental para las pruebas de hipótesis que verás más adelante.

Varianza y Desviación Muestral

La varianza muestral (s²) se calcula dividiendo la suma de desviaciones al cuadrado entre $n-1$: s² = Σ$xi-x̄$²/$n-1$. Para nuestro ejemplo: [(1-2)² + (2-2)² + (3-2)²]/(3-1) = 1 kg².

Existe una fórmula alternativa más práctica: s² = $Σxi² - n(x̄)²$/$n-1$. Con los mismos datos: [14 - 3(4)]/2 = 1 kg². Ambas fórmulas dan el mismo resultado.

La desviación muestral (s) es simplemente la raíz cuadrada de la varianza: s = √1 = 1 kg. Esta tiene las mismas unidades que tus datos originales, lo que la hace más fácil de interpretar.

Los gráficos con barras de error son súper útiles en investigación. Muestran la media como una barra vertical y la variabilidad como líneas que se extienden hacia arriba y abajo.

Tip profesional: Estos gráficos aparecen constantemente en revistas científicas - saber interpretarlos te dará ventaja.

Estadística Descriptiva Completa

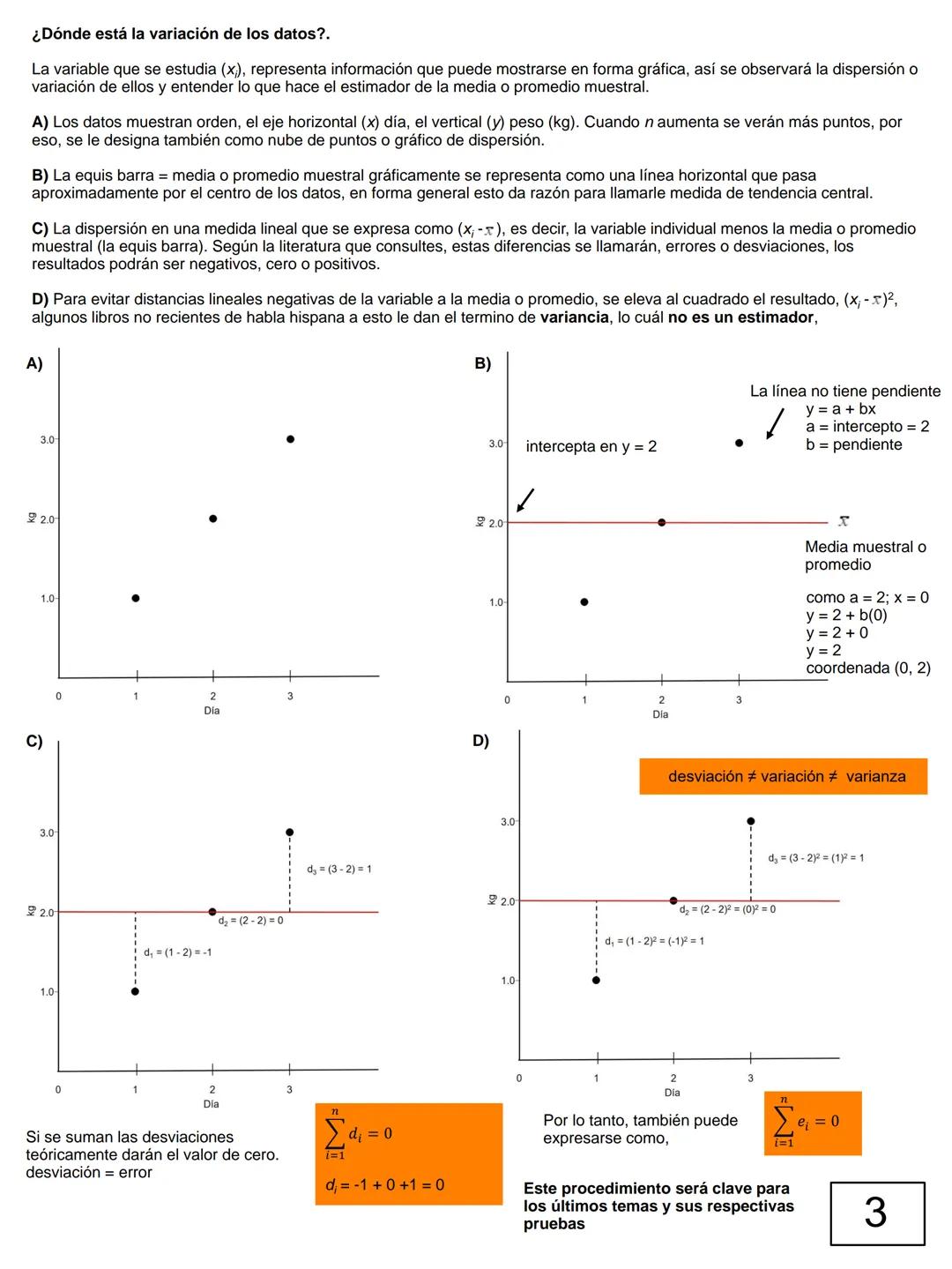
Además de la media, necesitas conocer otros estimadores importantes. El rango $máximo - mínimo$ te da una idea rápida de la dispersión total de tus datos.

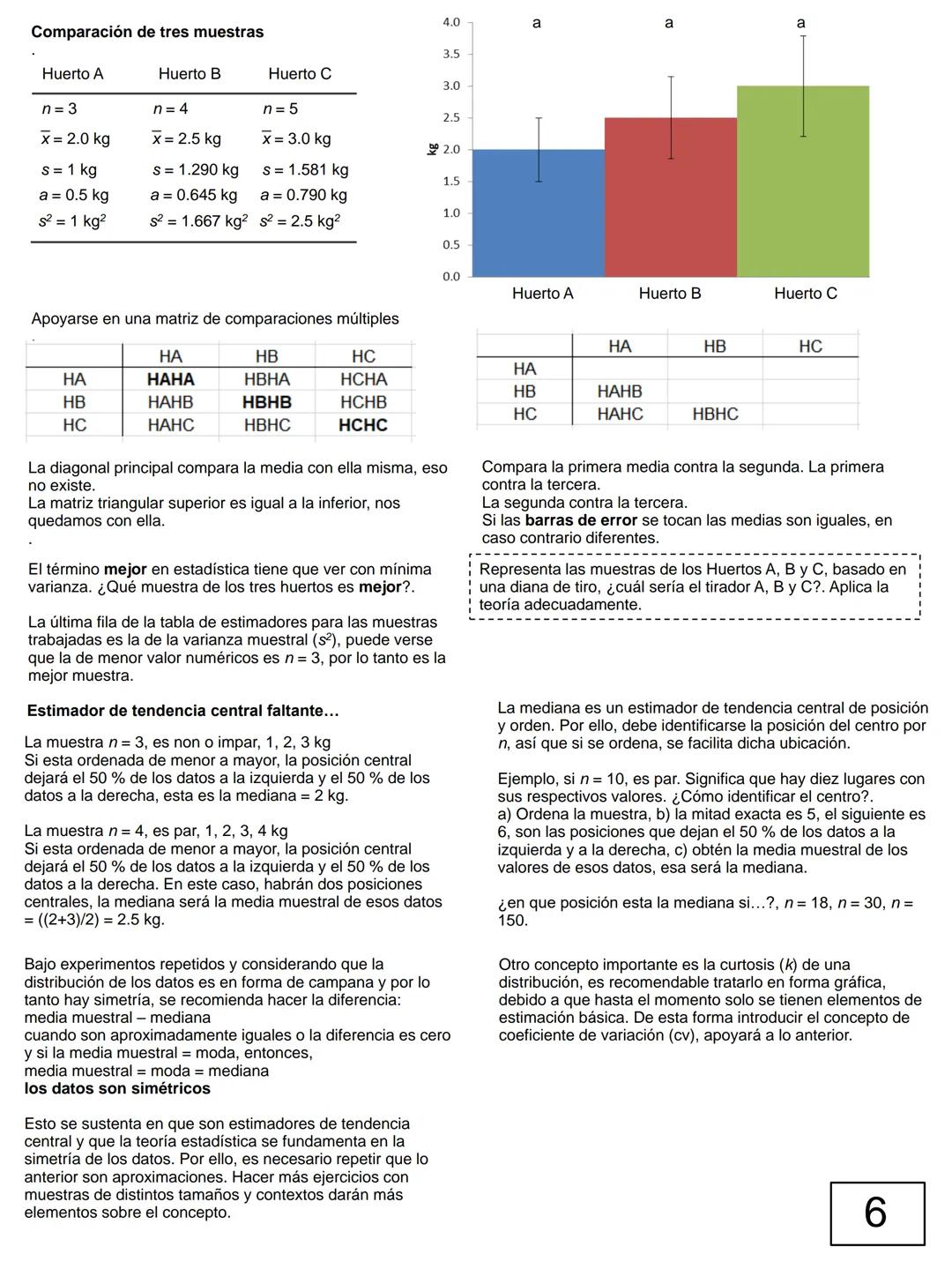
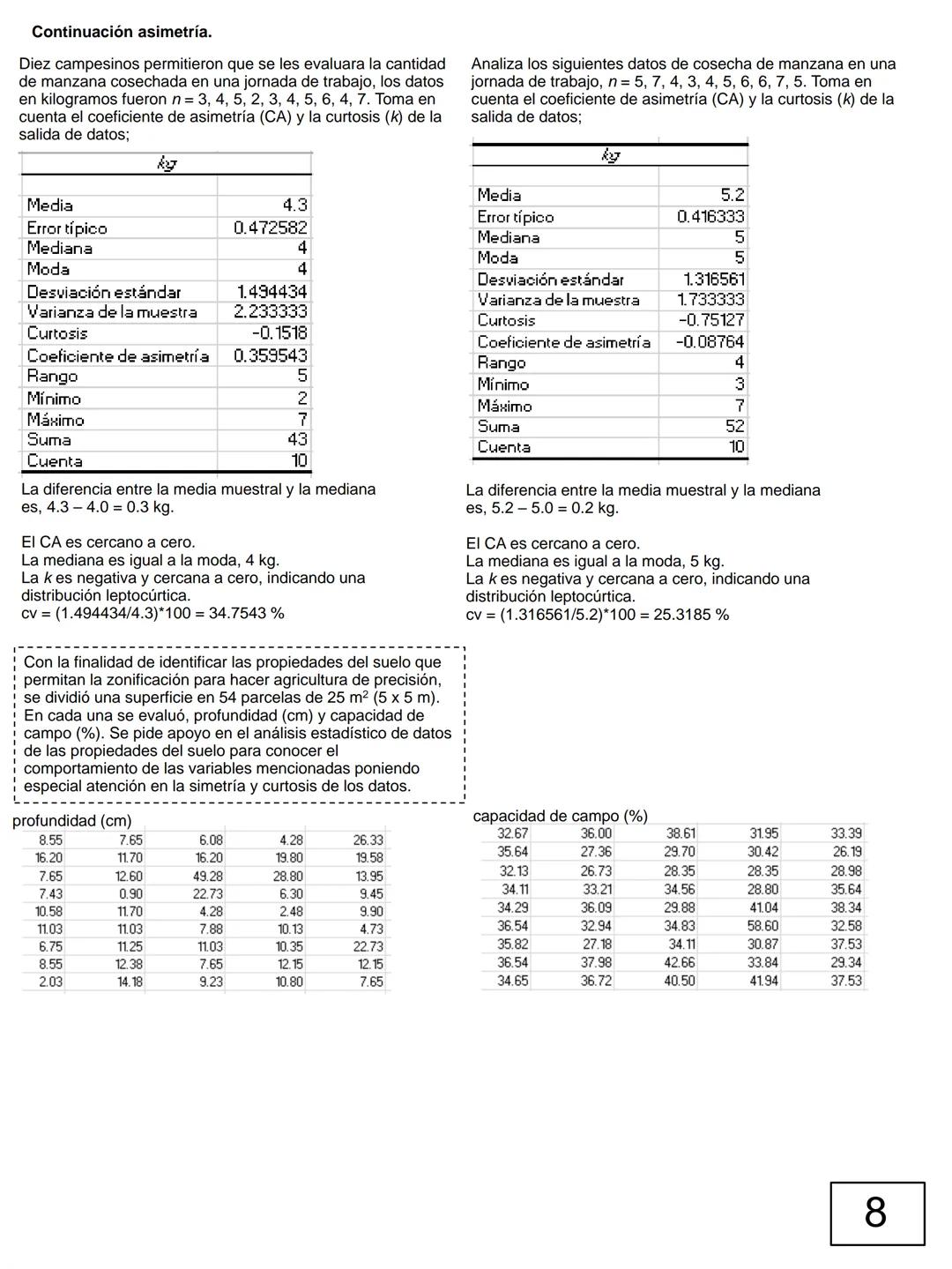
La moda es el valor que más se repite, mientras que la mediana es el valor central cuando ordenas tus datos. Si tu muestra tiene distribución simétrica, estos tres estimadores deberían ser muy similares.

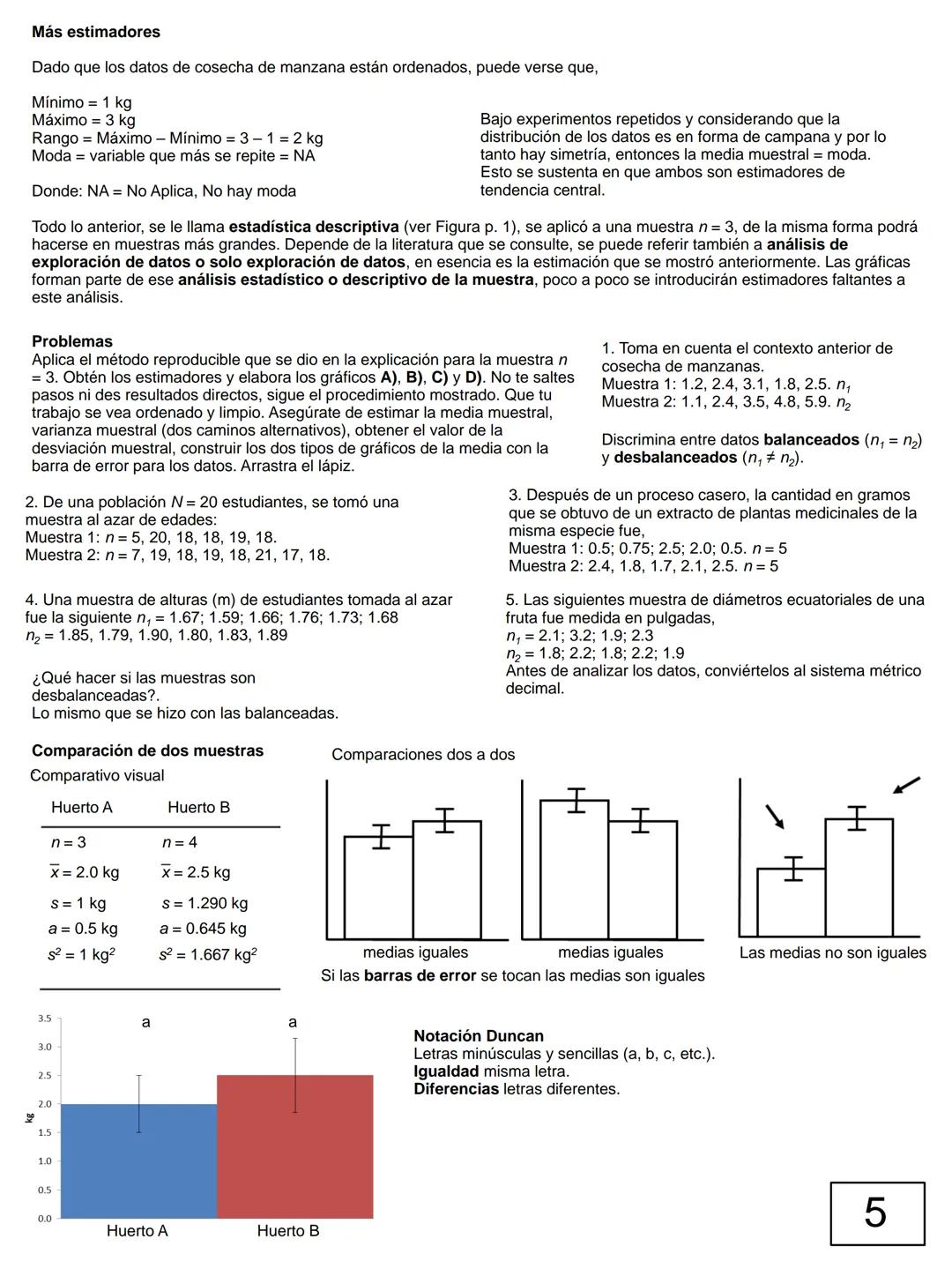
Cuando comparas muestras balanceadas (mismo tamaño) vs. desbalanceadas (diferente tamaño), el procedimiento es el mismo. La diferencia está en la interpretación y en el poder estadístico de tus conclusiones.

Para comparar grupos, usa la regla visual: si las barras de error se tocan, las medias son estadísticamente similares. Si no se tocan, hay diferencias significativas.

Concepto clave: La muestra con menor varianza es técnicamente "mejor" porque es más precisa y confiable.

Comparaciones Múltiples y Mediana

Cuando comparas tres o más grupos, necesitas una matriz de comparaciones. Esto evita conclusiones erróneas y te da un panorama completo de las diferencias entre grupos.

La mediana es un estimador de posición súper robusto. Para muestras impares $n=3$, es simplemente el valor central. Para muestras pares $n=4$, es el promedio de los dos valores centrales.

La simetría de datos se verifica comparando media, mediana y moda. Cuando media ≈ mediana ≈ moda, tus datos tienen distribución simétrica - ideal para la mayoría de análisis estadísticos.

Regla práctica: En datos simétricos puedes usar cualquier medida de tendencia central. En datos asimétricos, la mediana es más confiable que la media.

Asimetría y Coeficiente de Variación

El coeficiente de asimetría (CA) te dice si tus datos están sesgados. CA > 0 indica sesgo positivo (cola derecha), CA < 0 indica sesgo negativo (cola izquierda), y CA = 0 indica simetría perfecta.

La curtosis (k) describe la forma de tu distribución. k > 0 es leptocúrtica (puntiaguda), k = 0 es mesocúrtica (normal), y k < 0 es platicúrtica (aplanada).

El coeficiente de variación (CV) = $s/x̄$ × 100% te permite comparar variabilidad entre muestras con diferentes unidades o magnitudes. Un CV del 50% significa que la desviación es la mitad de la media.

Aplicación práctica: El CV es especialmente útil para comparar la precisión de diferentes métodos de medición o experimentos.

Análisis Avanzado de Asimetría

Con muestras más grandes $n=10$, los patrones de asimetría y curtosis se vuelven más evidentes y confiables. Observa cómo pequeñas diferencias entre media y mediana pueden indicar tendencias importantes.

El coeficiente de variación te ayuda a comparar la variabilidad relativa entre diferentes experimentos. Un CV menor indica mayor precisión y consistencia en tus mediciones.

Para datos de campo reales (como las 54 parcelas de suelo), necesitas prestar especial atención a la simetría y curtosis. Estos parámetros te dirán si puedes aplicar técnicas estadísticas que asumen normalidad.

Consejo de campo: Siempre revisa la simetría antes de elegir tus métodos de análisis - esto puede hacer la diferencia entre conclusiones correctas e incorrectas.